Common spatial patterns: Derivations
The common spatial patterns (CSP) algorithm [1, 2] is a popular supervised decomposition method for the EEG signal analysis which is used to distinguish between two classes (conditions). It finds spatial filters that maximize the signal variance for one class, while simultaneously minimizing the signal variance for the opposite class. Here, we review the CSP algorithm and its two main implementation approaches.
We assume that the EEG is already band-pass filtered and centered. Let ![]() be the EEG signal of trial
be the EEG signal of trial ![]() where
where ![]() is the number of channels and
is the number of channels and ![]() is the number of samples per trial. We compute the spatial covariance
is the number of samples per trial. We compute the spatial covariance ![]() by averaging over trials of class 1:
by averaging over trials of class 1:
(1) 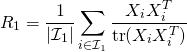
where
The goal of CSP is to find a decomposition matrix ![]() that projects the signal
that projects the signal ![]() in the original space to
in the original space to ![]() as follows:
as follows:
(2) ![]()
with the following properties:
(3) ![]()
(4) ![]()
and scaling such that
(5) ![]()
where
Columns of
Geometric approach
We determine whitening transformation matrix ![]() for composite spatial covariance
for composite spatial covariance ![]() such as
such as
(6) ![]()
We factorize composite spatial covariance
(7) ![]()
where
(8) ![]()
and transform matrices
(9) ![]()
We factorize matrix
(10) ![]()
where
(11) ![]()
Then this
(12) ![]()
and also 4 using 5
(13) ![]()
Generalized eigenvalue problem approach
We can directly solve ![]() by getting
by getting ![]() from 5 [3]:
from 5 [3]:
(14) ![]()
as
(15) ![]()
and by inserting this into 3
(16) ![]()
we get
(17) ![]()
which is an equation of generalized eigenvalue problem. Or equivalently, by inserting
(18) ![]()
Another solution
We also mention another solution ![]() (with different diagonal values
(with different diagonal values ![]() and
and ![]() ), which is often present in the literature, that satisfies only 3 and 4 but not 5. We get
), which is often present in the literature, that satisfies only 3 and 4 but not 5. We get ![]() from 3 as
from 3 as
(19) ![]()
and by inserting this into 4
(20) ![]()
we get
(21) ![]()
which is a generalized eigenvalue problem. This solution has different eigenvalues.
(22) ![]()
with
[Bibtex]
@article{Muller-Gerking1999,
abstract = {We devised spatial filters for multi-channel EEG that lead to signals which discriminate optimally between two conditions. We demonstrate the effectiveness of this method by classifying single-trial EEGs, recorded during preparation for movements of the left or right index finger or the right foot. The classification rates for 3 subjects were 94, 90 and 84{\%}, respectively. The filters are estimated from a set of multi-channel EEG data by the method of Common Spatial Patterns, and reflect the selective activation of cortical areas. By construction, we obtain an automatic weighting of electrodes according to their importance for the classification task. Computationally, this method is parallel by nature, and demands only the evaluation of scalar products. Therefore, it is well suited for on-line data processing. The recognition rates obtained with this relatively simple method are as good as, or higher than those obtained previously with other methods. The high recognition rates and the method's procedural and computational simplicity make it a particularly promising method for an EEG-based brain–computer interface.},
author = {M{\"{u}}ller-Gerking, Johannes and Pfurtscheller, Gert and Flyvbjerg, Henrik},
doi = {10.1016/S1388-2457(98)00038-8},
issn = {13882457},
journal = {Clinical Neurophysiology},
month = {may},
number = {5},
pages = {787--798},
publisher = {Elsevier},
title = {{Designing optimal spatial filters for single-trial EEG classification in a movement task}},
url = {https://www.sciencedirect.com/science/article/pii/S1388245798000388 https://linkinghub.elsevier.com/retrieve/pii/S1388245798000388},
volume = {110},
year = {1999}
}[Bibtex]
@article{Blankertz2008,
author = {Blankertz, Benjamin and Tomioka, Ryota and Lemm, Steven and Kawanabe, Motoaki and Muller, Klaus-robert},
doi = {10.1109/MSP.2008.4408441},
issn = {1053-5888},
journal = {IEEE Signal Processing Magazine},
number = {1},
pages = {41--56},
title = {{Optimizing Spatial filters for Robust EEG Single-Trial Analysis}},
url = {http://ieeexplore.ieee.org/document/4408441/},
volume = {25},
year = {2008}
}[Bibtex]
@article{Parra2005,
abstract = {In this paper, we describe a simple set of “recipes” for the analysis of high spatial density EEG. We focus on a linear integration of multiple channels for extracting individual components without making any spatial or anatomical modeling assumptions, instead requiring particular statistical properties such as maximum difference, maximum power, or statistical independence. We demonstrate how corresponding algorithms, for example, linear discriminant analysis, principal component analysis and independent component analysis, can be used to remove eye-motion artifacts, extract strong evoked responses, and decompose temporally overlapping components. The general approach is shown to be consistent with the underlying physics of EEG, which specifies a linear mixing model of the underlying neural and non-neural current sources.},
author = {Parra, Lucas C. and Spence, Clay D. and Gerson, Adam D. and Sajda, Paul},
doi = {10.1016/j.neuroimage.2005.05.032},
issn = {10538119},
journal = {NeuroImage},
month = {nov},
number = {2},
pages = {326--341},
publisher = {Academic Press},
title = {{Recipes for the linear analysis of EEG}},
url = {https://www.sciencedirect.com/science/article/pii/S1053811905003381 https://linkinghub.elsevier.com/retrieve/pii/S1053811905003381},
volume = {28},
year = {2005}
}